REVIEW: Lectures on the Icosahedron and the Solution of the Fifth Degree, by Felix Klein

Lectures on the Icosahedron and the Solution of the Fifth Degree, Felix Klein (Trübner & Co., 1884).

Raise your hand if you spent your childhood wondering why the world has three spatial dimensions. I hope that’s all of you, because it’s really very odd once you stop to think about it. Isn’t three an awfully arbitrary number? Why not two? Or four? Or Seven thousand two hundred and sixty eight? What’s so special about three?

It turns out that three is actually extremely special. For starters, planetary orbits are only stable in the presence of small perturbations because gravity obeys an inverse-square force law (this is called Bertrand's theorem). Yeah, yeah, Mr. Einstein, I know gravity doesn’t really do that. But it does approximately, and the reason that approximation works out in our universe is itself related to three-dimensionality.¹ So a universe with more or fewer spatial dimensions would be a fragile place, with planets forever zooming off into the depths of interstellar space or spiraling into the sun.

That gives a funny sort of anthropic argument for a three-dimensional universe, but it doesn’t satisfy me. Do you really think God couldn’t have figured out a way to bring forth intelligent life in a universe that lacked planets? Seems like a lack of imagination. Here’s an argument that actually moves me: without three spatial dimensions, there would be no music. For those of you too lazy to slog through that link, you start with Hadamard’s 1923 proof that distortionless wave propagation is only possible in a space with an odd number of dimensions. Then you do a little bit of math and show that if you add the requirement that the wave be radially symmetric, then it only works in dimensions one and three. But one-dimensional waves propagate without attenuation, so a one-dimensional universe would be “unbearably noisy.” Therefore music can only exist in three dimensions. QED.

So three dimensions actually are special from the perspective of physics (the two things I mentioned above aren’t exhaustive, there’s tons of stuff like this). But when we transcend carnality and enter the pure world of the forms, threeness gets even more special! There are a huge number of theorems that are trivial in every dimension but three or four, but in one or both of those cases are either really tricky or don’t work at all. Haters and losers will say this is because mathematics is something we invent, and our three-dimensional minds have been shaped by evolution to love questions that are interesting in three-dimensions. Anybody who says this has never met a mathematician.

Most examples of this specialness require too much background for me to explain, but here’s one that doesn’t. Remember the regular polygons? Equilateral triangles, squares, regular pentagons, etc.? These are shapes whose sides and angles are all the same. It’s pretty obvious that you can construct one with any number of sides, at least in two dimensions. But you can generalize the idea of a regular polygon to any number of dimensions — the result is called a “regular polytope,” and in every dimension five and up there are always exactly three of them. An infinite number of dimensions all have this in common, with this one big exception, and once again it’s our old friend three (and its next-door neighbor four).

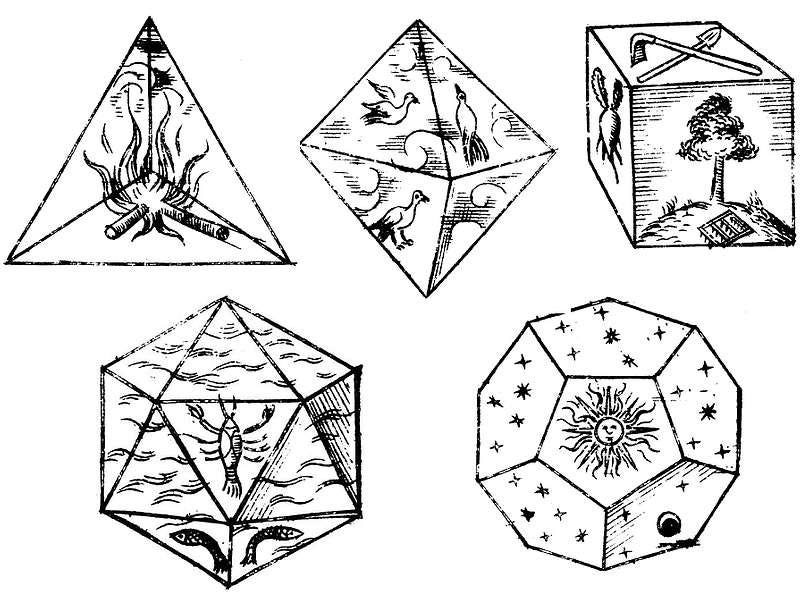
In three dimensions those regular polyhedra are called the Platonic solids,² and they’ve fascinated us for millennia. Plato wasn’t their discoverer,³ but he popularized them by producing a whole dialogue about their properties, and by confidently determining which regular polyhedron was the constituent of which element. For example, earth must be made up of tiny cubes, because it’s solid and difficult to move around, whereas fire must be made up of invisible tetrahedra, because it burns, and the vertices of a tetrahedron are pointy and sharp. In this way, Plato portrays a cosmos made up not of atoms, but of tetrahedra, cubes, octahedra, dodecahedra, and icosahedra. And he thereby anticipates much of contemporary mathematical physics (but we’re getting ahead of ourselves).

The alchemists were naturally all over the Platonic solids, but the next person to do something rigorous with them was Kepler. One of the chief virtues of a great scientist is the ability to notice a regularity in nature, form a wild hunch based on it, and dishonestly bludgeon the data until it fits the hunch. Often this misfires, but occasionally it produces something beautiful, and then…there are also the beautiful misfires. One such was Kepler’s Mysterium Cosmographicum. For each of the Platonic solids, you can imagine blowing a balloon inside of it until it just touches the faces of the solid, and also slowly deflating a much larger balloon around it until it just touches the vertices. The ratio of the radii of the inner balloon and the outer balloon is the same no matter how big or small the solid is, it’s just a fundamental property of that solid.

Now, the imaginative leap: Kepler noticed that these ratios are the same as the ratios between the orbits of successive planets in the solar system (well, sort of). The conclusion practically writes itself: the Ancients were correct that the Platonic solids make up everything, but overly literal in their application. It isn’t that fire is literally made up of tiny tetrahedra, but rather that the tetrahedron and its siblings govern the motion of the planets and the harmony of the heavens. Given the accuracy of the telescope technology available to Kepler, the model actually fit very well (you can play around with it on this website). We should consider ourselves lucky that Kepler leapt to this conclusion, because it was in trying to work out the kinks in this theory that he formulated his laws of planetary motion.

All of which finally brings us to this book. Felix Klein (yes, the guy who gave us Klein bottles) wrote an entire book about the icosahedron. That may seem like an odd choice, but in fact the icosahedron is very special.⁴ To see this, we need to step up a level in abstraction and stop thinking of the Platonic solids as shapes, and start thinking of them as self-contained families of symmetries (the mathematical term is “groups”). For any shape, in any dimension, we can consider all possible ways of acting on it which leave it unchanged — the ways of flipping it, rotating it, etc., where if you just had a before and after photo, you would have no way of proving it had moved at all.

This type of perspective shift — moving from consideration of a thing in itself, to the set of ways of acting upon a thing, or the implied relationships between a thing and all other things, is a very common trick in modern mathematics. It’s a powerful technique because it can both reveal properties of a thing that were hidden, and also cause distracting and irrelevant details of a thing to melt away. In the case of the Platonic solids, the shift to thinking of them as groups of symmetry transformations causes us to realize that there are actually only 3 of them! When you turn shapes into groups, the cube and the octahedron turn into the same one. A moment’s thought, and you realize it had to be true — if you imagine taking a cube, and turning all of its vertices into faces and all of its faces into vertices, the result is an octahedron. So they must have the same symmetries, and they really are, in some sense, the “same” thing, or perhaps two different physical incarnations of the same underlying idea.

Just as the cube and the octahedron are secretly the same, so are the dodecahedron and the icosahedron secretly the same.⁵ That may all be well and good, but I promised you that the icosahedron was special, and what about the “solution of the fifth degree” part of the title of this book? Most pop mathematics Substacks would simply point you at the deep connection between the icosahedron/dodecahedron and the golden ratio⁶ and be done with it. But I have higher expectations of my audience, so let’s try to get to the good stuff.

It all goes back to Galois theory. The groups of symmetries of the tetrahedron, and of the cube/octahedron, can be built up from the most elementary sorts of symmetries (mirror flips and simple planar rotations) in an especially simple way. It turns out that via Galois’ Rosetta Stone, this is exactly the quality that the symmetry group of an equation (all the ways you could permute the variables in an equation and have it stay the same equation) needs to have in order for it to be solvable with a formula that you can write down with algebraic symbols.

The symmetry group of the icosahedron/dodecahedron does not have this quality: it’s sort of analogous to a prime number in the world of symmetries, it can’t be neatly factored into pieces. This would be a mere curio, were it not for the fact that the 60 rigid rotations of an icosahedron correspond precisely to the 60 ways of performing an even number of swaps on a set of 5 objects (mathematicians call this group “A5”). But in general a fifth-degree equation has five solutions, and the most symmetric such equations will remain the same under any permutation of those solutions, so its symmetry contains A5, the symmetry of the icosahedron, inside of it, in a very special way. But since A5 cannot be factored, the symmetries of this equation can’t be either, and therefore there are fifth-degree equations with no algebraic solution.

A lot of people (including me) will speak imprecisely, and say something like, “Galois theory is the reason you can’t write a general quintic equation.” But actually, Galois theory is just the technique we use to prove it. The real reason is that the symmetries of the icosahedron, the 60 ways to rotate one and leave it looking the same, have this nontrivial internal structure. And it isn’t just fifth-degree equations. For every degree of polynomial five and up, there are equations whose symmetry groups contain A5 lurking inside them, an indigestible core blocking the way to solvability by radicals. The icosahedron is a magical portal connecting geometry to algebra — it may look like just a humble 3D solid figure, but it turns out to have a deep connection to which equations can and can’t be written down.

So that’s why Klein is interested in icosahedra, but this book isn’t about that impossibility (which was already well known by the time Klein was writing). Instead, Klein decides to take this immovable obstacle, and turn it into an opportunity. The general fifth-degree equation cannot have an algebraic solution, because of its special connection to the symmetries of an icosahedron, but Klein is able to take that same special connection and flip it around. He uses those very same symmetries of the icosahedron to find a non-algebraic approach to solving the quintic. His solution is a monster — a teetering tower of transcendental elliptic functions that would have been totally impractical to evaluate when he wrote them down. But now you can do it in a hundred lines of Python. You can find other, more modern expositions of the general idea here and here, and an alternative, purely iterative method here.

We’ve seen that the Platonic solids (and especially the icosahedron/dodecahedron) are quite important indeed, but I can’t help but feel that if we went back in a time machine and told Plato and Kepler all of this, they’d still be a smidge disappointed. Our ancestors dreamed that these mighty polyhedra controlled the elements of creation and the orbits of the planets, and what we’ve found is that they sort of control the kinds of equations we can write. Let’s be real, that’s a bit of a downgrade. But I have one more trick up my sleeve. Let’s see if we can’t still do Plato proud.

I’ve been worried for this entire book review that it’s been one giant exercise in what I call “string theory is like a taco”-syndrome. But now we’re about to talk actual string theory, and it’s going to get so much worse, so let me just put cards on the table: this next part I don’t know well enough to explain competently, let alone well enough to explain in simple terms. Even if I did know it well enough to explain it, you probably don’t know enough to understand an explanation in any but the most impressionistic sense. There is a real danger here that I’m going to end up telling you that string theory is like a taco. But string theory is not like a taco, string theory is like an icosahedron!

We’ve talked about the symmetries of shapes, and then the symmetries of solutions to equations, but modern physics is also all about symmetries — this time they’re symmetries in the laws of nature. Some of these are symmetries in the colloquial sense that you’re used to — for example if you flipped every object in the universe through a mirror, some of our theories of physics would just keep working.⁷ But others are symmetries in the more general sense of “a transformation of the whole system that leaves it unchanged in some important sense.” For example, taking every object in the universe and moving it 1 foot to the left is a symmetry the way physicists talk about it, but not in the sense that grade-schoolers do.

These symmetries (which for historical reasons are called “gauge invariance”⁸ by physicists) are at the heart of almost every bit of theorizing that modern physicists do. One of the deepest results of 20th century physics was the discovery that there’s an exact correspondence between symmetries in the laws of nature on the one hand, and conserved quantities on the other. And one of the hardest-won practical discoveries has been that every successful law of physics can be expressed in a pseudo-teleological form. So in practical terms, the way a lot of physics gets done is by proposing a pseudo-teleological law with the right sorts of symmetries, and then working out its consequences and seeing if they make any sense.

This is a little funny, because it’s the opposite of the inductive approach that science is “supposed” to follow. Rather than observe phenomena and try to figure out what law gave rise to them, we instead posit laws that are mathematically convenient and have roughly the right structure, and draw out their conclusions to see if they line up with reality. If you’ve ever snickered at the string theorists with their 8-dimensional and 11-dimensional theories, this is the style of argument that those theories came out of (and maybe don’t snicker, because it worked very well for general relativity).

If your goal is to come up with a Theory of Everything — something that unifies all the forces of nature, all the particles ever discovered, everything, all of it into one big equation — well, that thing is going to have a lot of symmetries. Many of the most promising candidate Theories of Everything start out by assuming that the symmetries of the laws of nature are subsumed by a fiendishly complicated mathematical object called “E8”. Other theories use slightly simpler younger siblings of E8, named E7 and E6 (there are no E1 through E5, don’t ask).⁹ You can’t visualize E8, because it’s 248-dimensional, but you can visualize its root system, which looks like this:

You may ask what’s so special about E6, E7, and E8. Why base string theory on these objects? Why not find some other ones, either slightly more or slightly less complicated? The answer is that there aren’t any others. Just as there are only five (really three) regular polyhedra in three dimensions, there are only three “exceptional simple Lie groups” in the E-family. This is not a coincidence. In mathematics there are very few coincidences. Something called the McKay correspondence links these Lie groups to the regular 3D solids.¹⁰ And as we’ve seen, there are three of those: the tetrahedron, the cube/octahedron, and the dodecahedron/icosahedron. If string theory or supersymmetry or some of these other Theories of Everything ever work out, it may indeed turn out to be the case that regular solids control the universe, and that fire is made up out of tiny, invisible tetrahedra. Plato would be pleased.

1. The math behind that is too hard for me to explain in this book review, but if you’re curious, check out this paper.

2. If you’re curious about their weird four-dimensional cousins, this page is a good place to start.

3. Even human beings weren’t their discoverer. Viruses love Platonic solids — many of them look like adorable little infectious polyhedra. Why? Because when you’re only carrying around a few kilobytes worth of genome, being able to build your body out of a single repeating pattern saves a ton of space.

4. If you want more ways it’s special besides the thing I’m talking about, check out this page or this one.

5. What about the tetrahedron? Well, imagine taking a tetrahedron and turning each of its faces into a vertex and each of its vertices into a face — the result is just another tetrahedron! We say it is “self-dual”.

6. The video that link points to is actually great. He has sequels about the numbers 8 and 24 that are more mathematically challenging but also great.

7. But fascinatingly enough, our very best theories of physics would not keep working unless you also reversed the direction of time and turned all the matter into antimatter and vice versa.

8. This language always confused me, but I think it comes from gauge in the sense of “measuring gauge.” Like if you changed your measuring gauge such that if it used to read 1 it now reads 2, and if it used to read 2 it now reads 3, and so on, then this is an example of the kind of symmetry transformation I mentioned. Because all you’ve changed is your gauge, the universe remains the same. But the flip side of this is that any transformation of the universe which could be interpreted as a transformation of your gauge, must necessarily be a transformation that leaves the laws of physics unchanged.

9. If you insist. These weird letter + number codenames come from the Cartan-Killing classification, often simply called the “Killing form,” after its discoverer, Wilhelm Killing. If I ever get around to writing a mathematical murder mystery, “the Killing form” would be a pretty good title.

10. Well, actually it links them to the finite subgroups of the rotations of a sphere, but it’s really easy to show that that’s exactly the same thing as the regular polyhedra (not easy enough to do in this review though).